Physical Oceanography
Physics of the Ocean
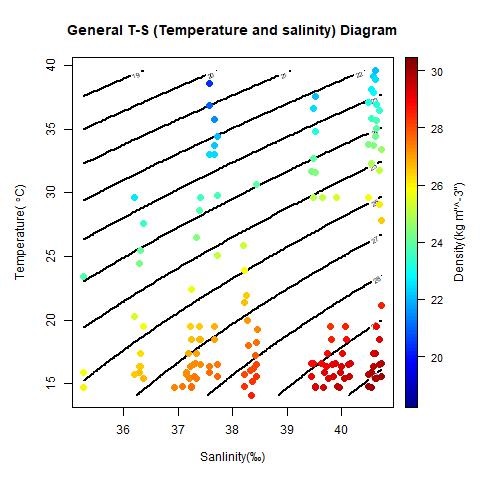
Seawater property means its temperature, salinity, pressure, density, viscosity, conductivity, specific heat, freezing point, and surface tension, etc. so seawater can be characterized by its temperature, salinity, and pressure, those can be calculated by various methods, equations, and toolboxes. The GSW Oceanographic Toolbox of TEOS-10 is one of the most famous toolboxes.
Julia is a high level ,high performmance ,dynamic programming language. Today , I like to use Julia for sea water
properties analysis. I have published a medium post over this with details explanation. I will use GibbsSeaWater julia package. Installation code here,
using Pkg
Pkg.add("GibbsSeaWater")
here the my medium post link
Contents of this Notebook
- Calculating practical salinity
- Calculating conductivity from practical salinity
- Calculating practical salinity from reference salinity
- Calculating conservative temperature from in-situ temperature
- Calculating potential temperature of ice from the potential enthalpy of ice
- Calculating in-situ density, the appropriate thermal expansion coefficient, and the appropriate saline contraction coefficient of seawate
- Calculating the potential density of anomaly with reference pressur
- Calculating ratio of practical salinity to conservative temperature
- Calculating conservative Temperature of the maximum density of seawater
- Calculating latent heat of evaporation of water from seawater
print("hafez \n")
print("Hello Julia, I want to analyze the sea water property ")
using GibbsSeaWater
- Calculating practical salinity: Calculates Practical Salinity, SP, from conductivity, C, primarily using the PSS-78 algorithm.
C=[56.6, 56.0,57.7] #conductivity (mS/cm)
T=[6.7,8.8,8.0] #in situ temperature[deg C]
P=[10.0,50.0,125.0] #sea pressure [dbar]
sp=gsw_sp_from_c.(C,T,P)
2. Calculating conductivity from practical salinity
SP = [34.5487,34.7275,34.8605,34.6810, 34.5680, 34.5600,]
t = [28.7856, 28.4329,22.8103, 10.2600, 6.8863, 4.4036,]
p = [ 10,50,125,250,600,1000]
c=gsw_c_from_sp.(SP,t,p)
3.Calculating practical salinity from reference salinity
sr =[28.9,28.4,34.23] #reference salinity
sp=gsw_sp_from_sr.(sr)
4.Calculating conservative temperature from in-situ temperature
sa=[34.5,34.8] # absolute salinity [g/kg]
t=[28.78,22.39]
p=[10.0,50.0]
ct=gsw_ct_from_t.(sa,t,p)
5.Calculating potential temperature of ice from the potential enthalpy of ice
p_en_ice=[-3.44e5,-3.6e5] # potential enthalpy of [j/kg]
pto_ice=gsw_pt_from_pot_enthalpy_ice.(p_en_ice)
6.Calculating in-situ density, the appropriate thermal expansion coefficient, and the appropriate saline contraction coefficient of seawater
ct=[34.5,35.05] # conservative temperture
sa=[28.8,22.7] # absolute salinity
p=[10.0,50.0] # sea pressure
rlb=gsw_rho_alpha_beta.(sa,ct,p)
println(rlb)
7.Calculating the potential density of anomaly with reference pressure
ct=[34.5,35.05] # conservative temperture
sa=[28.8,22.7] # absolute salinity
sigmaO=gsw_sigma0.(sa,ct)
8.Calculating ratio of practical salinity to conservative temperature
SA = [34.7118, 34.8915, 35.0256, 34.8472, 34.7366, 34.7324]
CT = [ 3.7856, 3.4329, 2.8103, 1.2600, 0.6886, 0.4403]
p = [ 10.0, 50.0, 125.0, 250.0, 600.0, 1000]
t_Ih = [-10.7856, -13.4329, -12.8103, -12.2600, -10.8863, -8.4036] # in situe temperature of the ice ath p pressure p
melting_ice_SA_CT_ratio=gsw_melting_ice_sa_ct_ratio.(SA,CT,p,t_Ih)
9.Calculating conservative Temperature of the maximum density of seawater
rho=[1021.86,1022.26] # density of seawater [kg/m²]
ct=[28.2,22.05] # conservative temperture
p=[10.0,50.0] # sea pressure
sa=gsw_sa_from_rho.(rho,ct,p)
10.Calculating latent heat of evaporation of water from seawater
ct=[28.2,22.05] # conservative temperture
sa=[28.8,22.7] # absolute salinity
latentheat_eva_Ct=gsw_latentheat_evap_ct.(sa,ct)